|
A 1.0 |
Die Parabel p hat die Gleichung
y = 0,25x2 + x + 1,5 mit
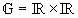 . .
|
|
|
|
A 1.1
|
Berechnen Sie
die Koordinaten des Scheitelpunktes S der Parabel p.
Zeichnen Sie sodann die
Parabel p im Bereich
-8 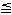 x x 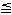 4
in ein Koordinatensystem. 4
in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit 1 cm;
-9 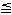 x x 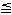 7 ;
-1 7 ;
-1 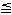 y y 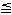 10 10
|
3 P |
|
|
|
A 1.2 |
Punkte An(x | -0,25x2 + x + 1,5)
und Punkte Cn liegen auf der Parabel p und sind zusammen
mit den Punkten Punkte Bn und Dn die
Eckpunkte von Quadraten
AnBnCnDn.
Die Abszisse der Punkte Cn ist stets um 4 größer als die Abszisse x
der Punkte An.
Zeichnen Sie
die Quadrate A1B1C1D1
für x = -7 und A2B2C2D2
für x = 0 in das Koordinatensystem zu 1.1 ein.
Zeigen Sie sodann, dass für
die Koordinaten der Punkte Cn in Abhängigkeit von der
Abszisse x der Punkte An gilt:
Cn(x + 4 | 0,25x2 + 3x + 9,5)
|
3 P |
|
|
|
A 1.3 |
Stellen Sie den Flächeninhalt A(x)
der Quadrate AnBnCnDn in
Abhängigkeit von der Abszisse x der Punkte
An dar.
[Ergebnis: A(x) = (2x2 + 16x + 40)FE ]
|
3 P |
|
|
|
A 1.4 |
Unter den Quadraten
AnBnCnDn
besitzt das Quadrat
A0B0C0D0
den kleinsten Flächeninhalt.
Berechnen Sie diesen kleinstmöglichen Flächeninhalt Amin.
|
1 P |
|
|
|
A 1.5 |
Bei den Quadraten A3B3C3D3
und
A4B4C4D4
beträgt die Seitenlänge jeweils 5 LE.
Berechnen Sie
die x-Koordinaten der Punkte C3 und C4
auf zwei Stellen nach dem Komma gerundet.
|
3 P |
|
|
|
A 1.6 |
Die x-Achse schließt mit der Symmetrieachse A5C5 des Quadrates
A5B5C5D5
den Winkel j mit dem Maß 35° ein.
Hinweis: yA5 < yC5
Berechnen Sie
die x-Koordinaten der Punkte A5 auf
zwei Stellen nach dem Komma gerundet.
|
3 P |
|
|