|
Nutzungshinweis |
Durch Anklicken der fettgedruckten Begriffe
erhältst Du Lösungen bzw. Lösungshinweise.
Viel Erfolg bei der anstehenden
Abschlussprüfung!
|


|

|
Abschlussprüfung 2004 Mathematik II Gruppe A Aufgabe 1
|

|
|
|
|
A 1.0 |
Die Parabel p hat eine Gleichung der Form
y = ax2 + 0,5x + c mit
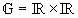 , aÎIR\{0}
und cÎIR. Die Parabel p verläuft
durch die Punkte P(-1|-4) und Q(5|-7). Die Gerade g hat die Gleichung
y = -0,5x + 3 mit , aÎIR\{0}
und cÎIR. Die Parabel p verläuft
durch die Punkte P(-1|-4) und Q(5|-7). Die Gerade g hat die Gleichung
y = -0,5x + 3 mit 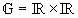 . .
|
|
|
|
A 1.1
|
Zeigen Sie durch Berechnung der Werte a und c, dass die Parabel p
die Gleichung
y = -0,25x2 + 0,5x -3,25 hat.
Erstellen Sie für die Parabel p eine Wertetabelle für
xÎ[-3;5] in Schritten von
Dx = 1 und zeichnen Sie die
Parabel p und die Geraden g in ein Koordinatensystem.
Für die Zeichnung: Längeneinheit 1 cm;
-4 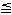 x x 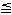 9 ;
-9 9 ;
-9 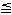 y y 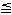 5 5
|
4 P |
|
|
|
A 1.2 |
Punkte An(x | -0,25x2 +0,5x - 3,25)
auf der Parabel p und Punkte Dn(x | -0,5x + 3) auf der Geraden g
haben jeweils die gleiche Abszisse x. Sie bilden zusammen
mit den Punkten Bn und Cn Eckpunkte
von Trapezen AnBnCnDn
und es gilt:
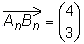 , , 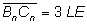 und [AnDn] || [BnCn].
und [AnDn] || [BnCn].
Zeichnen Sie
die Trapeze A1B1C1D1
für x = -1 und A2B2C2D2
für x = 4 in das Koordinatensystem zu 1.1 ein.
|
2 P |
|
|
|
A 1.3 |
Überprüfen Sie rechnerisch,
ob die Gerade A1B1 Tangente an die Parabel p ist.
[Teilergebnis: A1B1: y = 0,75x - 3,25]
|
3 P |
|
|
|
A 1.4 |
Zeigen Sie durch Rechnung, dass sich die Seitenlänge
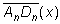 aller Trapeze AnBnCnDn
in Abhängigkeit von der Abszisse x der Punkte An wie folgt darstellen lässt: aller Trapeze AnBnCnDn
in Abhängigkeit von der Abszisse x der Punkte An wie folgt darstellen lässt:
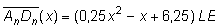
|
1 P |
|
|
|
A 1.5 |
Stellen Sie den Flächeninhalt A(x)
der Trapeze AnBnCnDn in
Abhängigkeit von der Abszisse x der Punkte
An dar.
Berechnen Sie sodann den kleinstmöglichen Flächeninhalt Amin.
[Teilergebnis: A(x) = (0,5x2 - 2x + 18,5)FE ]
|
3 P |
|
|
|
A 1.6 |
Unter den Trapezen AnBnCnDn gibt
es zwei Trapeze A3B3C3D3 und
A4B4C4D4, in denen der Winkel
A3D3C3
bzw. A4D4C4 jeweils
das Maß 90° hat.
Begründen Sie, dass für diese
beiden Trapeze gilt: 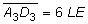 bzw.
bzw. 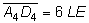 . .
Berechnen Sie sodann die x-Koordinaten der Punkte A3 und A4 auf
zwei Stellen nach dem Komma gerundet.
|
3 P |
|
|
|
|
 |
(c) A. Meier, 2004 |
 |
|
|